Strategic Value Investing: Dividend Discount Models
"This basic model is applied by many professional investors, both from the value and growth camps... The application of the model, specifically estimating the parameters, is what leads some investors to be successful and others to struggle and make regrettable decisions."
That quotation comes from chapter seven of "Strategic Value Investing: Practical Techniques of Leading Value Investors," a book that digs deeply into the foundations of value investing.
As the title suggests, authors Stephen Horan, Robert R. Johnson and Thomas Robinson explored the use of present value, which can be computed by using dividend discount or discounted cash flow models.
They added that the model is both theoretically and practically sound, but like all other models, is subject to the "garbage in, garbage out" rule.
Present value
One of the keys to understanding this model is to know the concept of present value:
"Central to the concept of investing is the most basic concept of finance: present value. Simply stated, present value is the fundamental principle that a dollar received today is worth more than a dollar received tomorrow. Likewise, a dollar to be received tomorrow is worth more than a dollar received in two days. The rationale is that a dollar received today can be invested to earn interest and will be worth more at a later date."
For example, if the current interest rate is 3%, then the present value of one dollar due to be received in one year will be 97.09 cents. If you were not expecting to get that dollar back for 10 years, then its present value would be 74.41 cents, according to the formula.
The authors added, "The critical concept to present value is that once dollars to be received in the future are discounted back to a present value, they can be added together to determine the value of a series of future cash flows (CF)." Because of present value, adding current dollars and future dollars is akin to adding apples and oranges. To avoid that, future dollars are converted to current dollars, then added together.
The formula states that the value of an investment is the sum of all future cash flows, discounted back to present values; in mathematical terms, it looks like this:

This formula works for all forms of investments, including stocks, bonds, real estate and more. The future cash flows may be dividends, bond coupons or rents from a real estate asset. The authors wrote, "The valuation model is simple. The art of investing comes with estimating both the magnitude of the future cash flows and the appropriate interest (or discount) rate."
In a sidebar, they also note that so-called "new paradigms," like the one circulating in the late 1990s, claimed that present value no longer matters. In the 1990s, it was a belief that present value was outdated and needed to be replaced with metrics that valued companies according to "new economy" criteria such as "click-throughs" and "eyeballs." The crash of 2000 promptly scuttled those ideas.
Getting back to the main argument, they provided the example of a bond that will pay out a lump sum of $1,000 in three years and provide annual interest payments of $50 per year. What is its present value and what you would be willing to pay for it?
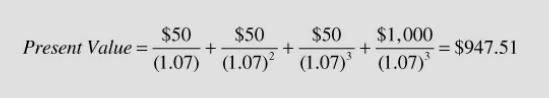
There's also the example of a stock that pays an annual dividend of $3 and is expected to be worth $50 in three years. What is the present value of that stock, assuming the discount (interest) rate is 7%?
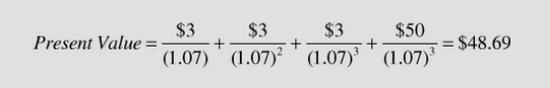
While simple and straightforward, the authors had a warning about present value models: "Remember, these models are meant to provide an approximation of value and not a precise value to the penny. Often, when models are made more complicated it gives the user the illusion of precision."
It's simple and easy to work with simple models--when the circumstances are simple. As the circumstances become more complex, models need to evolve with them. For example, how do you calculate an infinite series of constantly increasing dividends?
Professor Myron Gordon's constant growth dividend discount model
This model is the most commonly used stock valuation model and is widely taught. It deals with the problem posed above and works well for companies that have stable dividend growth.
This example shows the formula applied to General Electric (NYSE:GE) in 2012:
The current dividend was 70 cents.
Interest/discount rate: 11%
The growth rate of future dividends: 7%
Thus:

Many might assume that extrapolating such a growth rate into infinity is unrealistic, and they would be right. Ironically, that turned out to be true for General Electric, which has fallen upon hard times in recent years; its annual dividend in 2012 was 68 cents and it subsequently increased to 96 cents before ignominiously collapsing to 4 cents last December.
For a more realistic model, one in which a company is expected to do very well for a few years and then plateau after maturing, analysts use the two-stage dividend growth model.
The two-stage dividend growth model
This is based on the idea of an "abnormal" dividend growth rate in the short term, followed by a "normal" growth rate in the long term. Behind this model is the theory that companies go through an industry life cycle made up of four phases: pioneer, growth, mature and decline. The abnormal rate is applied to the growth stage, and normal for the mature and decline stages.
Therefore, investors expect two distinct flows of cash:
The present value of dividends received during the abnormal growth period.
The present value of dividends received during the normal growth period.
If this model reminds you of the Gordon constant growth model, that's because it is nearly the same. And, indeed, the Gordon model is often incorporated into the two-stage model. According to the authors, "Since the dividends are assumed to grow at a constant rate after three years, we can apply the Gordon constant growth model to find the stock value at that time."
Sensitivity analysis is a valuable complement to dividend discount models. It alerts investors to the potential implications of small changes in the growth rate or the discount rate. Again, higher sensitivity should lead to wider margins of safety.
Conclusion
To find the intrinsic value of a stock, it's necessary to figure out how much the stock will return to investors in coming years. Yet, a dollar received tomorrow is worth less than a dollar in hand today. To deal with this irregularity, the dividend discount or DCF model was developed.
Within the model, there are two submodels, the Gordon growth model and the two-stage growth model. Each can help investors develop a reasonable estimate of present value and intrinsic value. As noted, remember that the models deliver approximations of value, not precise, to-the-penny valuations.
Read more here:
Not a Premium Member of GuruFocus? Sign up for a free 7-day trial here.
This article first appeared on GuruFocus.
Warning! GuruFocus has detected 3 Warning Signs with GE. Click here to check it out.
This Powerful Chart Made Peter Lynch 29% A Year For 13 Years
How to calculate the intrinsic value of a stock?
